
Mean, Median & Mode (বিখ্যাত তিনজন তারকার গল্প)
পরিসংখ্যানের দুনিয়ায় দুইটা চমকপ্রদ শব্দ হচ্ছে পপুলেশন এবং স্যাম্পল। বলতে গেলে পরিসংখ্যানের দুনিয়াটা শুরুই হয় এদের দিয়ে। এরা গলাগলি করে জীবন যাপন করে। বলতে পারেন কাউকে ছাড়া কেউ বাঁচবে না এই টাইপ। চলুন, দেখা যাক কি কারণে এদের মধ্যে এত ভালবাসা।
জুতার দোকানে গেলেই কোন না কোন জুতা ঠিক আপনার পায়ে লেগে যাচ্ছে। জিন্সের প্যান্ট,শার্ট বা যেকোন জামা কিনতে গিয়েছেন, ঠিকই নিজের মাপের প্যান্ট বা শার্ট পেয়ে যাবেন। প্রশ্ন হল আপনার মাপ দোকানদার কিভাবে পেল? অবশ্যই আপনি দেন নি, তাহলে কি কেউ আপনার তথ্য বিক্রি করল? ( ভয়ানক ব্যাপার হয়ে যাবে তাহলে!! ) এই প্রশ্নের উত্তর হল কেউই আপনার মাপ জানে না, কেউই আপনার তথ্য বিক্রি করে নি। আমাদের এই দুনিয়াতে এই মুহুর্তে প্রায় ৭.৫৩ বিলিয়ন মানুষ বেঁচে আছে। ধরুন আপনি এবার ভাবলেন জুতার কোম্পানি দিবেন। তাহলে আপানর লক্ষ্য কারা? আমাদের এই ৭.৫৩ বিলিয়ন মানুষ, তাই না? এর বাইরে কি আর কেউ আছে? নাই তো ( এলিয়েনের জন্য পরে চিন্তা করেন ভাই ! ) তাহলে আপনার ডাটাসেটের এই মোট জনসংখ্যাকে পরিসংখ্যানের ভাষায় বলে পপুলেশন। একটু সুন্দর করে বললে আমাদের কাছে যদি কোন ডাটাসেট থাকে তাহলে পুরো ডাটাসেটকে আমরা বলি পপুলেশন। কি, ক্লিয়ার তো? বেসম্ভব ক্লিয়ার করতে হবে। আচ্ছা এবার ভেবে দেখুন আপনি কি এই ৭.৫৩ বিলিয়ন মানুষের সবার পায়ের মাপ নিয়ে জুতা বানাবেন? চাইলে করতে পারেন, তবে জুতার কোম্পানি আর দেয়া লাগবে না। কিন্তু আপনি জানেন, আপনার মাথায় অনেক বুদ্ধি। আপনি খেয়াল করে বের করলনে যে প্রতি ১০০০ জন লোকের মাঝে ১০০ জন লোকের পায়ের মাপ একই ( ধরে নিলাম ) । তাহলে একজনের মাপ নিয়ে আপনি ১০০ জনের জুতা বানাতে পারবেন। একই ভাবে মাত্র ১০ জনের মাপ নিয়ে আপনি ১০০০ জনের জন্য জুতা বানাতে পারবেন। আপনার কাছে মোট ছিল ১০০০ জন লোক, মাপ নিলেন মাত্র ১০ জনের, যা আসলে মোট লোকের একটা ছোট্ট অংশ। এবার বলুন তো ৭.৫৩ বিলিয়ন মানুষের পায়ের মাপ নেয়ার জন্য কি আপনি সবার পা মেপে বেড়াবেন? অবশ্যই না। আপনি একটি অংশের মাপ নিবেন। এই যে সব মানুষের মাপ না নিয়ে একটা ছোট্ট অংশের মাপ নিয়ে নিলেন, এই ছোট্ট অংশকেই বলে স্যাম্পল। একটু সুন্দর করে বললে আমাদের যে ডাটাসেট দেয়া থাকবে তার যেকোন একটা অংশকে স্যাম্পল বলে।
তাহলে কি আমরা বলতে পারি স্যাম্পল আসলে পপুলেশনের একটা অংশ? অবশ্যই পারি।
একটা ছোট্ট ডাটাসেট কল্পনা করি যা এরকমঃ [ American, American, Indian, Indian, Bangladeshi, Bangladeshi, Bangladeshi, Bangladeshi ] ধরলাম এই সেটে ৮জন মানুষের জাতীয়তার তথ্য আছে। কেউ আমেরিকান, কেউ ইন্ডিয়ান আর কেউ বাংলাদেশি। খেয়াল করুন আমাদের এই ডাটাসেটে আমেরিকান, ইন্ডিয়ান এবং বাংলাদেশি ছাড়া আর কোন জাতি নাই। তাহলে আমরা দেখতে পাচ্ছি আমেরিকান ২ জন, ইন্ডিয়ান ২ জন এবং বাংলাদেশি মোট ৪ জন আছে। এখানে American, Indian, Bangladeshi আমাদের ডাটাসেটের ইউনিক ভ্যালু। কারণ এরা ছাড়া আর কেউ নেই। প্রতিটা ইউনিক ভ্যালু ঠিক কতবার করে আছে, এই ব্যাপারটাকে বলা হয় ডাটাসেটের ফ্রিকুয়েন্সি। মনে হচ্ছে না, খুব সহজ একটা ব্যাপার? কিন্তু এই সহজ ব্যাপারটা আপনাকে ডাটার এই যুদ্ধে অনেকখানি এগিয়ে রাখবে সব সময়। আপনি যখন আপনার ডাটাসেটের ফ্রিকুয়েন্সি জানেন এর মানে হল, আপনি ডাটাসেট সম্পর্কে অর্ধেক জেনে গিয়েছেন।
চলুন এই ফ্রিকুয়েন্সির কোড একটু দেখে আসিঃ
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
data = ['American','American','Indian','Indian','Bangladeshi','Bangladeshi','Bangladeshi','Bangladeshi']
dataset = pd.DataFrame(data=data,columns =['Nationality'])
dataset_frequnecy = dataset['Nationality'].value_counts()
print(dataset_frequnecy)
dataset_frequnecy.plot(kind='bar', rot=45, grid=True)
plt.show()
উপরের কোডটুকু রান করালে আমরা এরকম একটা আউটপুট পাবো। ছবিটা দেখে এই ছোট্ট ডাটাসেট সম্পর্কে আমরা বেশ একটা ধারণা পেয়ে যাই।
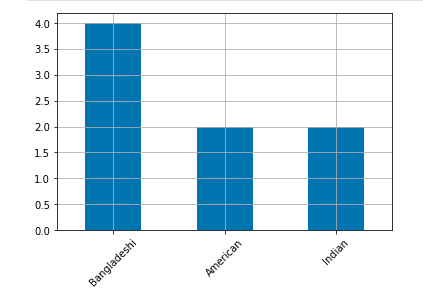
একটা ডাটাসেট আসলে অনেক টাইপের ডাটা দিয়ে ভরপুর থাকতে পারে। তার মধ্যে যদি সংখ্যা থাকে তাহলে ব্যাপারটা কিছুটা পেট খালি করে কাচ্চি খাওয়ার মত হয়ে যায়। কারণ ডাটাসেটের ডাটা যদি নিউমেরিক হয় তাহলে আপনার জন্য তথ্য জানা এবং তথ্য খুঁজে বের করা সবচেয়ে উপযোগী একটা ব্যাপার। পপুলেশন, স্যাম্পল এবং ফ্রিকুয়েন্সির পর সবচেয়ে বড় আলোচ্য যে বিষয় সেটা হল আপনার ডাটা থেকে সারমর্ম জেনে নেয়া এবং ডাটাসেটের রিপ্রেজেজেন্টিভ ভ্যালু খুঁজে বের করা। সারমর্ম জানার জন্য ডাটা নিউমেরিক হওয়া আবশ্যক (তবে না হলেও তারজন্যে ব্যবস্থা আছে)। ডাটার সারমর্ম জানা যায় পরিসংখ্যান জগতের তিন তারকার সাহায্যে। এরা হল গড় (Mean), মধ্যক (Midean) এবং প্রচুরক (Mode) । চলুন এই তারকাদের গল্প শুনা যাক।
গড় (Mean):
শুরুতে একটা ছোট্ট ডাটাসেট নিয়ে নিচ্ছি। ধরলাম আমাদের কাছে আছে [০,১,৪,৭,৮,১০] । আমরা সবাই জানি যে ডাটার গড় কিভাবে বের করতে হয়। তাও আরেকবার বলে নিচ্ছি। ধরলাম আমাদের কাছে n সংখ্যক ডাটা রয়েছে। তাহলে আমাদের প্রথমে n সংখ্যক ডাটা যোগ করতে হবে এবং যোগফলকে n দিয়ে ভাগ করতে হবে। প্রাপ্ত ফলাফলই আমাদের গড় । কথা হচ্ছে এই গড় এর মাহাত্ম্য কোথায়? আমরা ছোট্ট একটা ডাটাসেট নিয়েছি। ধরে নিচ্ছি এটা ৬ জন বন্ধুর কাছে বর্তমানে টাকার পরিমাণ। এর গড় করলে আমরা পাবো (০+১+৪+৭+৮+১০)/৬ = ৫, যার অর্থ দাড়ায় ৬ জন বন্ধুর প্রত্যেকের কাছে ৫টাকা আছে বা তার চেয়ে কিছু কম বা বেশি আছে। তাহলে কি বুঝা গেল? আমরা যেহেতু গড় জানি , তাই আমরা এখন আমাদের ডাটাসেটের সব ভ্যালু সম্পর্কে একটা মুটামুটি সারমর্ম জানতে পেরেছি, যে কার কাছে কত টাকা থাকতে পারে। তাই না?
আমাদের প্রাপ্ত গড়কে যদি একটা সংখ্যারেখায় বসানো যায় তাহলে দেখতে উপরের ছবিটার মত হবে। দেখুন, আমরা যে গড় পেয়েছি তা আমাদের ডাটাসেটের ঠিক মাঝামাঝি একটা সংখ্যা। আরেকটু ভাল করে খেয়াল করলে দেখবেন যে আমাদের ডাটাসেটের ডাটা থেকে গড়ের দূরত্ব খুব বেশি নয়। সর্বোচ্চ দূরত্ব (৫-০) = ৫ বা (১০-৫) = ৫ এবং সর্বনিম্ন দূরত্ব (৫-৪) = ১। এই কারণগুলার জন্য আমরা আমাদের গড় ৫ কে আমাদের ডাটাসেটের রিপ্রেজেন্টিভ ভ্যালু বলতে পারি। তবে সব সময় যে গড়, ডাটাসেটের একদম মাঝেই হবে তা নয় কিন্তু। এই ডাটাসেটের [০,২,৩,৩,৩,৪,১৩] গড় বের করে দেখুন, দেখবেন গড় যেকোন একদিকে সরে গেছে।
দাঁড়ান দাঁড়ান !! আগের গড় রিপ্রেজেন্টিভ কিন্তু এইটা কি রিপ্রেজেন্টিভ? ভাবুন। তাহলে এই ডাটাসেটের গড় কি ভুল? আসলে এতক্ষণ গড় নিয়ে যা বলে আসলাম তা ছিল এর বাহ্যিক কিছু রূপ। কিন্তু গড় আসলেই কি করে তা বুঝার জন্য আপনি প্রথমেই ধরে নিবেন গড় আমাদের ডাটাসেটের এমন এক জায়গার একটা ভ্যালু যে জায়গা থেকে গড়ের চেয়ে কম ভ্যালুর দূরত্ব এবং গড়ের চেয়ে বেশি ভ্যালুর দূরত্ব একই। বুঝেন নি? বুঝাচ্ছি, দাঁড়ান!!
আমাদের প্রথম ডাটাসেটের গড় ছিল ৫। ৫ এর চেয়ে কম সংখ্যা গুলো হচ্ছে ০,১,৪ এবং বড় সংখ্যা গুলো হচ্ছে ৭,৮,১০। তাহলে ছোট সংখ্যা গুলো থেকে দূরত্ব বের করি। (৫-০) + (৫-১) + (৫-৪) = ১০ । এবার বড় সংখ্যাগুলোর থেকে দূরত্ব বের করি। (৭-৫) + (৮-৫) + (১০-৫) = ১০। কি দেখলেন? দুই দিক থেকে একই দূরত্ব। এবার পরে আময়রা আরেকটা ডাটাসেট নিয়েছিলাম [০,২,৩,৩,৩,৪,১৩] , এর গড় হল ৪। ৪ এর চেয়ে কম সংখ্যা হল ০,২,৩,৩,৩ । এদের দূরত্ব বের করিঃ (৪-০) + (৪-২) + (৪-৩) + (৪-৩) + (৪-৩) = ৯ । ৪ এর চেয়ে বড় সংখ্যা হল ১৩। দূরত্বঃ (১৩-৪)=৯। তাহলে আময়রা দেখলাম ডাটাসেটের গড় আসলে এমন এক ভ্যালু যা ডাটাসেটের এক ব্যালেন্স অবস্থায় থাকে এবং যা ডাটাসেটের সব ভ্যালুকে একটা সার্বজনীন রূপ দেয়। যদি এখনো গড় না বুঝে থাকেন তাহলে নিচের ছবিটা দেখুনঃ
একটা লাঠির উপর এক এক জায়গায় এক এক পরিমাণ ভার আছে। কিন্তু লাঠিটি ৪ নাম্বার বিন্দুতে একদম স্থির বা ভারসাম্য অবস্থায় থাকতে পারে। সহজ ভাষায় বলতে গেলে ৪ নাম্বার বিন্দুর ডান দিকের ওজন এবং বাম দিকের ওজন যদি সমান হয় তাহলেই কেবল লাঠিটি ৪ নাম্বার বিন্দুতে স্থির থাকবে। তাই না? কিন্তু ৪ নাম্বার বিন্দুতে তো ওজন ৪। আবার লাঠির ওই সকল বিন্দুতে যদি সম পরিমাণ ভার থাকে তাহলেও লাঠিটি ৪ নাম্বার বিন্দুতে স্থির থাকবে। আচ্ছা, তাহলে আমরা কি বলতে পারি লাঠিটি যেহেতু স্থির এবং গড় মান ৪ তাহলে লাঠির সব জায়গায় ৪ পরিমাণ ওজন আছে? অবশ্যই বলতে পারি। আর এখানেই গড়ের বিশাল মাহাত্ম্য।
মধ্যক (Median)
ধরুন আমাদের কাছে একটা ডাটাসেট আছে যার চেহারাটা এরকম [৫,৬,৭,৭, ১০ বা তার বেশি] । উপরের এত আলোচনা করার পর যদি এখন জিজ্ঞাসা করা হয় এই ডাটাসেটের রিপ্রেজেন্টিটিভ ভ্যালু বের করার জন্য তাহলে আপনার মাথায় সবার আগের গড় বের করার চিন্তা আসবে। গড় কিভাবে বের করতে হয় মনে আছে নিশ্চয়ই? চলুন বের করি। সংখ্যাগুলো যোগ করি ৫+৬+৭+৭+ ...... দাঁড়ান দাঁড়ান !! "১০ বা তার বেশি" এটা তো কোন সংখ্যা না, আবার ১০ এর বেশি অনেক কিছু হতে পারে। তাহলে এই ডাটাসেটে আমরা কি গড় বের করতে পারবো? না, পারবো না। তাহলে ডাটাসেটের রিপ্রেজেন্টিটিভ ভ্যালু বের করব কিভাবে? আমাদের ডাটাসেটে যখন এই ধরনের সমস্যার উদ্ভব ঘটে তখন আমরা আমাদের ডাটাসেটের ঠিক মাঝের ভ্যালুটাকে আমাদের রিপ্রেজেন্টিটিভ ভ্যালু হিসেবে নিয়ে নেই। ডাটাসেটের এই মাঝের ভ্যালুকে বলা হয় মধ্যক (Median) ।
তাহলে আমাদের এই ডাটাসেটের ঠিক মাঝের ভ্যালু হল ৭, যা আমাদের এই ডাটাসেটের রিপ্রেজেন্টিটিভ ভ্যালু। খেয়াল করুন আমাদের ডাটাসেটের মোট ডাটার সংখ্যা বিজোড় হওয়াতে খুব সহজেই আময়রা মাঝের ভ্যালু বুঝে নিতে পেরেছি। কিন্তু যদি জোড় হত তাহলে কিন্তু মাঝের ভ্যালু পেতাম ২টি। যেমন ধরা যাক [২,৪,৭,৭,৮,১০ বা তার বেশি] । যদি ডাটাসেটের ডাটা সংখ্যা জোড় হয় তাহলে মাঝের দুই ভ্যালুর গড়ই হল আমাদের ডাটাসেটের মধ্যক। অর্থাৎ (৭+৭)/২=৭।
এই মধ্যক এবং গড়ের একটা মজার ব্যাপার দেখা যাক। একটা ডাটাসেট চিন্তা করা যাক। [২,৩,৫,৫,১০] । এই ডাটাসেটের গড় ৫ এবং মধ্যক ৫। এবার শেষের ভ্যালু অর্থাৎ ১০ এর বদলে যদি ১০০০ বসাই তাহলে গড়ের মান বদলে হয়ে যায় ২০৩ কিন্তু মধ্যক পরিবর্তন হয় না। কি বুঝলেন? ডাটাসেটের মধ্যক পরিবর্তন হয়ে যদি ডাটাসেটের অন্য কোন ডাটা পরিবর্তন করা হয় তাহলেও মধ্যক পরিবর্তন হয় না। কিন্তু যেকোন ডাটা পরিবর্তন হলে গড় মানের পরিবর্তন আসে। এ কারণে মধ্যকে বলা হয় resistant or robust statistic।
প্রচুরক (Mode)
একদম শুরুতে আমরা একটা ডাটাসেট নিয়ে কাজ করেছিলাম। মনে আছে? [ American, American, Indian, Indian, Bangladeshi, Bangladeshi, Bangladeshi, Bangladeshi ]। আমরা দেখেছিলাম যে আমাদের এই ডাটাসেটে ইউনিক ভ্যালু হল American, Indian এবং Bangladeshi। কিন্তু এরা তো নিউমেরিক না। তাহলে এদের থেকে ডাটাসেটের সারমর্ম কিভাবে বের করব? গড় নাকি মধ্যক? একটাও তো সম্ভব না কারণ কোন সংখ্যাই নাই। কিন্তু আমাদের কাছে এই ডাটাসেটের ফ্রিকুয়েন্সি আছেঃ
- American - ২
- Indian - ২
- Bangladeshi - ৪
এখানে সর্বোচ্চ ফ্রিকুয়েন্সি হল ৪। ডাটাসেটের অবস্থা যদি এমন হয় যে সেখানে গড় বা মধ্যক কোনটাই বের করার উপায় থাকে না তখন আমরা সেখানে সর্বোচ্চ ফ্রিকুয়েন্সি বের করি। ডাটাসেটের এই সর্বোচ্চ ফ্রিকুয়েন্সিকে বলা হয় প্রচুরক বা Mode। একটা ডাটাসেটে কেবল একটা প্রচুরক থাকতে পারে, আবার দুইটা প্রচুরক থাকতে পারে আবার দুইয়ের বেশিও প্রচুরক থাকতে পারে। যদি একটা প্রচুরক থাকে তাহলে সেই ডাটাসেটকে বলা হয় unimodal distribution, যদি দুইটা প্রচুরক থাকে তাহলে তাকে বলা হয় bimodal distribution। আর যদি দুইয়ের বেশি থাকে তাহলে তাকে বলা হয় multimodal distribution। এখন একটা প্রশ্ন মনে খটখট করছে, আসলে ঠিক কি টাইপের ডাটার ক্ষেত্রে প্রচুরক বের করা উচিত? সাধারণত Nominal, Ordinal এবং Discrete টাইপের ডাটার ক্ষেত্রে প্রচুরক নিয়ে কাজ করা হয়, কারণ এদের ক্ষেত্রে কোন সাংখ্যিক মান পাওয়া যায় না।
এবার আসি কিছু গুরুত্বপূর্ন কথায়। একটা symmetrical ডাটাসেট যদি চিন্তা করি যেমনঃ [২,৩,৫,৫,১০] তাহলে সেক্ষেত্রে দেখা যাবে গড়, মধ্যক এর অবস্থান সব সময় একই অবস্থানে, এমনকি প্রচুরকও। তবে একাদিক প্রচুরক থাকলে সেক্ষেত্রে গড় ও মধ্যকের অবস্থান একই থাকবে কিন্তু প্রচুরকের অবস্থান ভিন্ন হবে। একটা চিত্রের সাহায্যে ব্যাপারটা পরিষ্কার করা যাকঃ
উপরের চিত্রে গড়, মধ্যক এবং প্রচুরকের অবস্থান একই এবং প্রচুরক মাত্র একটি।
উপরের চিত্রে গড়, মধ্যক এর অবস্থান একই কিন্তু প্রচুরক দুইটা থাকায় তাদের অবস্থান ভিন্ন। এমনও হতে পারে যে ডাটা সেটের কোন প্রচুরক নাই। তখন দেখতে কিছুটা এরকমঃ
প্রথম যে ছবিটা দেখা যাচ্ছে এই ধরণের ঘটনা তখনই ঘটবে যদি আমাদের ডাটাসেট Normal distribution হয়, দ্বিতীয় যে ছবিটা দেখা যাচ্ছে সেটি ঘটবে যখন আমাদের ডাটাসেট হবে symmetrical distribution আর তৃতীয় যে ছবিটি দেখা যাচ্ছে সেটি ঘটবে যদি আমাদের ডাটাসেট হয় Uniform distribution।
উপরের আলোচনা গুলো ছিল মূলত গড়, মধ্যক এবং প্রচুরক কি, কিভাবে কাজ করে ইত্যাদি। তবে আমাদের যদি ডাটাসেট থেকে এই তিন তারকার তথ্য বের করার প্রয়োজন হয় তবে সেটা আমরা পাইথনের pandas নামক লাইব্রেরি দিয়ে সহজেই করে ফেলতে পারি। নিচে ডাটাসেট থেকে গড়, মধ্যক এবং প্রচুরক বের করার কোড দিয়ে দিচ্ছিঃ
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
data = [1,1,1,2,2,3,6,6,6,6,6,6,8,9,10,10,10]
dataset = pd.DataFrame(data=data,columns =['money'])
print("Mean: {0}".format(dataset['money'].mean()))
print("Median: {0}".format(dataset['money'].median()))
print("Mode: {0}".format(dataset['money'].mode()))
আউটপুটঃ
Mean: 5.470588235294118
Median: 6.0
Mode: 0 6
dtype: int64
তো এই ছিল পরিসংখ্যান জগতের তিন তারকার গল্প, যাদের মাধ্যমে আজ ডাটা সাইন্টিস্টরা একটা ডাটাসেট থেকে অনেক সুন্দর সুন্দর তথ্য বের করে নিয়ে আসতে পারেন। সবাই ভাল থাকবেন।

