
Stack এবং ২০টা প্লেটের বাক্সের গল্প
Stack এক ধরনের লিনিয়ার ডাটা স্ট্রাকচার। আচ্ছা, লিনিয়ার একটা টেকনিক্যাল শব্দ তার সাথে ডাটা আবার তার স্ট্রাকচার… ওয়েট ওয়েট ওয়েট!! এক এক করে বুঝার ট্রাই করি।
Line বা রেখা তো সবাই চিনি? চেনার কথা! না চিনলেও সমস্যা নাই। আচ্ছা, হাতের কাছে কলম আছে তো? কলম নিয়ে সাদা পাতায় পাশাপাশি ছোট ছোট ১০-২০টা কালো বৃত্ত আঁকি। কিছুটা এরকম …………………………….
এই ছোট ছোট বৃত্তের মাঝে যে গ্যাপগুলা দেখা যায় সেগুলাতেও কয়েকটা বৃত্ত এঁকে দেই। এবার দূউউউউউরররর থেকে দেখার ট্রাই করি। কি দেখা যায়..হুম!
হ্যাঁ, তোমার মন ঠিক ধরতে পেরেছে। যা দেখা যায় সেটা একটা লাইন বা রেখা। ভদ্র ভাষায় বললে একটা সরল রেখা। তাহলে কি বুঝলে? একটা সরল রেখা আসলে পরপর অনেক গুলা বিন্দুর সমন্বয়ে তৈরী।
এবার যে বৃত্ত গুলা আঁকলে সেগুলার একটা একটা নাম দাও। তাহলে ধরলাম প্রথম পাঁচটা নাম যদু, মধু, কদু, লদু এবং বদু। এরা একজনের পিছনে আরেকজন দাঁড়ানো। যেহেতু এরা একজনের পিছনে অন্যজন দাঁড়ানো তাই বলা যায় যদুর সাথে সম্পর্ক ঠিক তার পরের জনের, যার নাম মধু। আবার মধুর সাথে সম্পর্ক তার দুই পাশে দুইজনের, অর্থাৎ যদু এবং কদুর। আবার কদুর সাথে সম্পর্ক তার দুই পাশের দুইজনের অর্থাৎ মধু এবং লদুর। তাহলে আমরা বলতে পারি একটা সরল রেখা যদি অনেক গুলা বিন্দুর সমন্বয়ে তৈরী হয় তাহলে প্রতিটা বিন্দু শুধুমাত্র তার দুইপাশের দুইজনের সাথেই যোগাযোগ বা সম্পর্ক রাখতে পারবে। উদাহরণ দেইঃ একটা সরল রেখাতে ধরলাম ১০০ টা বিন্দু আছে (ধরলাম আর কি!!)। তাহলে আমরা যা বুঝলাম সেই অনুযায়ী ৩ নাম্বার বিন্দু থেকে ১০ নাম্বার বিন্দুতে যাবার কোন সুযোগ নেই। ৩ নাম্বার থেকে শুধু মাত্র ২ এবং ৪ নাম্বার বিন্দুতেই যাওয়া সম্ভব।
এই যে সরল রেখার একটা নিয়ম এটাকেই লিনিয়ার সিস্টেম বলে। অর্থাৎ তুমি এই সিস্টেমে তোমার অবস্থান থেকে ঠিক পরের অবস্থানে বা ঠিক আগের অবস্থানে যেতে পারবে৷ হুট করে উড়াল পংখী দিয়ে লাফ দেয়া যাবে না।
এই তো গেল লিনিয়ার কি সেই কেচ্চা কাহিনী। এবার Stack …
আচ্ছা ধর, বাসায় ২০ জন মেহমান আসছে। তোমাদের বাসায় কাচ্চি রান্না হয়েছে, কোপাকোপি খাওয়া দিয়ে ২০টা প্লেট ময়লায় জর্জরিত। বাসার বুয়া ২০টা প্লেট ধুয়ে একের উপর এক রাখার সময় হঠাত তোমার একটা প্লেট নেয়ার প্রয়োজন। তুমি এবার কোন প্লেটটা নিবে? যেকোন একটা, নাকি সবার উপরে যেটা সেটা? অবশ্যই সবার উপরেরটা। অর্থাৎ যে প্লেট সবার শেষে রাখা হয়েছে সেটাই আগে তুলে নিবে। এবার এই ২০টা প্লেট কে ২০টা ডাটা চিন্তা কর, যেগুলাকে তুমি একের উপর এক সাজায়ে রাখছো। এবার তোমাকে আমি ওই ২০টা ডাটা থেকে একটা ডাটা দিতে বললাম। তুমিও আমাকে সবার উপরে যে ডাটা বা সবার শেষে যে ডাটা রাখছো (এই লাইন আবার পড়) সেটাই আমাকে দিবে। একটু সুন্দর করে বললে ডাটাসেটের Top element টাই সব সময় আগে বের হবে। তাই না? এই যে ডাটা রাখার একটা সিস্টেম জানলে, এটাই হল Stack। তাহলে যা যা জানলাম, তার একটা রিভিউ দেই। Stack এমন একটা ডাটা স্ট্রাকচার যেখানে আমরা ডাটা ইচ্ছামত রাখতে পারি যাকে বলে data push করা। কিন্তু ডাটা বের করার সময় সবার শেষেরটা বা top এর যে element শুধু সেটাই বের করতে পারবো। একটা element বের করার পরেই কেবল আমরা পরের element বের করতে পারবো। অর্থাৎ প্রথম top এ যে আছে সে বের হবার পর, পরের জনকে আমরা বলতে পারি আমাদের নেক্সট Top element। কি, বুঝলা তো!!
একটু ছবি দেখে ব্যাপারটা আর ক্লিয়ার করি

প্রথম ছবিটা দেখ। বিভিন্ন কালারের অনেকগুলা লেয়ার একের পর এক সাজানো আছে। কালারফুল লেয়ার গুলোকে প্লেটের মত চিন্তা কর যেমন আগের উদাহরণে বলেছিলাম। কি? মাথায় এবার কিছু ঢুকল? না ঢুকলে টেনশন নেবার দরকার নাই। আরেকটা উদাহরণ দিচ্ছি। নিচের ছবিটা দেখ।
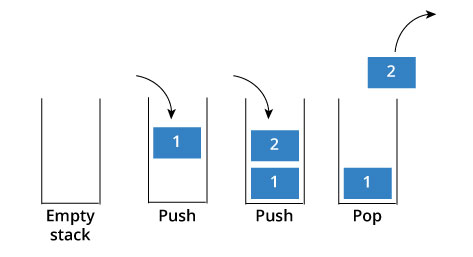
ধরলাম আমাদের প্লেট রাখার একটা বাক্স আছে। যাকে নাম দিয়েছি Empty stack। আমাদের কাছে যে ধুয়া প্লেট গুলো আছে সেগুলাকে আমরা নাম্বার দিলাম ১,২ এভাবে। এবার ১ নাম্বার প্লেট ধুয়ে প্রথমে বাক্সে রাখলাম। যেটাকে আসলে প্রোগ্রামিং এর ভাষায় বলে stack এ ডাটা push করা। তাহলে আমাদের stack এর Top element এখন ১ নাম্বার প্লেট। এবার ২ নাম্বার প্লেটকেও ধুয়ে আমাদের stack বাক্সে রাখলাম অর্থাৎ push করলাম। এখন তাহলে top element কে বল দেখি? হ্যাঁ , ঠিক। এখন top element ২ নাম্বার প্লেট। এভাবে একসময় ৩,৪,৫,৬,৭,৮ করে করে ২০টা প্লেট ধুয়া হয়ে গেলে একদম top element হবে ২০। এবার আসি প্লেট বের করা নিয়ে। বাক্স থেকে যদি প্লেট বের করি ( যাকে প্রোগ্রামিং এর ভাষায় বলে pop করা ) তাহলে সবার উপরে যে, মানে যে আমাদের top element তাকেই আগে বের করতে হবে। তাহলে আমরা প্রথমে ২০ নাম্বার প্লেট pop করলাম বা বের করলাম। তাহলে বাক্সে এখন আছে ১৯টা প্লেট এবং এখন top element হল ১৯। বুঝা গেল? এভাবে প্রতিবার যদি প্লেট pop কর মানে বের কর তাহলে পরের প্লেট হয়ে যাবে top element । না বুঝলে ছবি দেখে লেখাটা আবার পড়লে ঠিকই বুঝে যাবে।
আমরা তো শিখে গেলাম। এবার আরেকজনকে এই ব্যাপারটা শিখাইতে হবে। উনি হলে কম্পিউটার, দ্যা বস। উনি তো আবার কোড ছাড়া আমাদের কথা বুঝেন না। তাহলে একটু কোডে উনাকে এই stack জিনিষটা বুঝানো যাক। কোডিং এর অংশটা আমি পাইথনে লিখেছি। আশা করি বুঝতে সমস্যা হবে না।
আমাদের একটা বাক্স ছিল প্লেট রাখার। মনে আছে? সেই বাক্স বানানো যাক
def create_stack_box():
stack_box = []
return stack_box
আচ্ছা বাক্স তো বানায়ে ফেললাম। এবার কম্পিউটারকে শিখাই যে, বাক্সটা খালি কি না সেটা কিভাবে চেক করবে
def is_empty(stack_box):
return len(stack_box) == 0
এবার আমাদের stack বাক্সে কিভাবে প্লেট বা data push করবে সেটা শিখাই
def push_plate(stack_box, plate):
stack_box.append(plate)
print(plate + " pushed to stack box ")
এবার আমাদের stack বাক্স থেকে প্লেট বের করাটা শিখাই
def pop_plate(stack_box):
if (isEmpty(stack_box)):
return str(-maxsize -1)
return stack_box.pop()
যদি আমাদের বাক্সটা আগে থেকেই খালি হয় তাহলে আমরা বিশাল একটা নেগেটিব সংখ্যা ফেরত পাঠাবো
return stack_box.pop()
আর যদি আমাদের বাক্সে প্লেট থাকে তাহলে তো আমরা সবার উপরের প্লেটটা বের করে নিব
অনেক তো বাক্সে প্লেট রাখলাম ( push element) আবার বাক্স থেকে প্লেট বের করলাম ( pop element ) । এবার আমরা top element কে সেটা জানতে চাই
def peek_plate(stack_box):
if (is_empty()):
return str(-maxsize -1)
যদি আমাদের বাক্সটা আগে থেকেই খালি হয় তাহলে আমরা বিশাল একটা নেগেটিব সংখ্যা ফেরত পাঠাবো
return stack_box[len(stack_box) - 1]
প্রোগ্রামিং এ লিস্ট বা এরের নাম্বারিং শুরু হয় ০ থেকে। আবার top element বলতে আমরা সবার শেষেরটাকেই বুঝই। যার মানে হল লিস্ট বা এরের যা length তার চেয়ে এক কম যে index সেটাই হল সবার শেষ index । ব্যাপারটা বুঝে গেছ আশা করি ।
অনেক তো শিখাইলাম। এবার সবগুলাকে কাজে লাগাই। একের পর এক শিখানো নিয়মগুলা কম্পিউটারকে করতে বলি।
stack_box = create_stack_box()
push_plate(stack_box, str(10))
push_plate(stack_box, str(20))
push_plate(stack_box, str(30))
print("Top element of our stack_box is: {0}".format( peek_plate(stack_box) ))
print(pop_plate(stack_box) + " popped plate from stack_box")
পুরো কোডটা একসাথে দেখে নেই
from sys import maxsize
def create_stack_box():
stack_box = []
return stack_box
def is_empty(stack_box):
return len(stack_box) == 0
def push_plate(stack_box, plate):
stack_box.append(plate)
print(plate + " pushed to stack box ")
def pop_plate(stack_box):
if (is_empty(stack_box)):
return str(-maxsize -1)
return stack_box.pop()
def peek_plate(stack_box):
if (is_empty()):
return str(-maxsize -1)
return stack_box[len(stack_box) - 1]
if __name__ == "__main__":
stack_box = create_stack_box()
push_plate(stack_box, str(10))
push_plate(stack_box, str(20))
push_plate(stack_box, str(30))
print("Top element of our stack_box is: {0}".format( peek_plate(stack_box) ))
print(pop_plate(stack_box) + " popped plate from stack_box")
এই stack দিয়ে করেটা কি? কোটি টাকার প্রশ্ন ।
- Prefix, Postfix বা Infix notation এর এক্সপ্রেশন থেকে মান বের করার জন্য এই দারুণ ডাটা স্ট্রাকচার ব্যবহার করা হয়।
- প্রোগ্রামিং দুনিয়ায় ব্যাক-ট্র্যাকিং খুব দারুণ একটা জিনিস। যারা এটা নিয়ে কাজ করেছে তারা জানে এটা কতটা চ্যালেঞ্জিং আর কতটা মজার। এই ব্যাক-ট্র্যাকিং এ stack ডাটা স্ট্রাকচার ব্যবহার করা হয়।
- DFS (Depth First Search) গ্রাফ এলগোরিদমে এই stack কে ব্যবহার করা হয়।
- অনেক প্রোগ্রামিং প্রবলেম থাকেই stack নির্ভর। অর্থাৎ stack দিয়েই ওই প্রবলেম সলভ করতে হয়।
তো এই ছিল Stack এবং ২০টা প্লেটের বাক্সের গল্প। Happy Programming Life

